MENU
The Electronic Scholarly Publishing Project: Providing world-wide, free access to classic scientific papers and other scholarly materials, since 1993.
More About: ESP | OUR CONTENT | THIS WEBSITE | WHAT'S NEW | WHAT'S HOT
ESP Essays 07 Jan 2026 Updated:
Mendel's Work
Classical Genetics, II
Like begets like, more or less. Although this basic fact of heredity has been known since ancient times, the actual mechanisms of heredity, indeed, even the mathematical patterns of heredity, were completely unknown until Gregor Mendel did his breakthough work. When he published his findings in 1866, the scientific world failed to recognize their significance and the work was largely ignored, until it was rediscovered in 1900. Then, many recognized the huge potential in his findings, triggering an explosion of work that, in just two decades, laid the complete foundation of our modern understanding of genetics.
Mendel's Approach

Gregor Mendel, the founder of classical genetics.
By the mid-nineteenth century the fact of inheritance was well established. Animal and plant breeders had known for thousands of years that the attributes of the parent were important in determining the attributes of the offspring and they had routinely used that knowledge to increase the quality of their stocks. However, for all those years the mechanism of inheritance was not at all understood. One of the mistakes made by many early researchers was that they would often perform only one cross and then only examine the results from just one generation. Or, if they did follow the crosses for more than one generation, they almost never recorded the data separately for the different generations. In addition, these early workers almost never counted the numbers of different types of progeny that were produced.
In 1856 an Austrian monk, Gregor Mendel, began a study of heredity which employed several new techniques. When it was completed and published in 1865, it proved to be astonishingly accurate — with almost no substantial changes Mendel's ideas now constitute the foundations of the modern theory of genetics.
To see why Mendel was so successful when his predecessors failed, we must consider Mendel's approach to his research and the conceptual skills that he used in the analysis of his results. We will examine Mendel's work in some detail, because it provides an introduction to the study of genetics and to the experimental method. All of our modern knowledge of heredity rests upon the foundation of experimental science, and without an appreciation for the logic of scientific discovery there can be no real understanding of any scientific discipline.
An Aside on the Method of Science
Although there are many systems of belief that claim to offer explanations for the functioning of the physical universe, only one of these — science — contains within itself the rules by which its own most cherished and widely held beliefs are to be rejected. Science requires that each of its claims and statements be constantly subjected to test through experimentation — through a physical comparison of its predictions with actual reality. Beliefs that fail these tests are subject to doubt, and if legitimate explanations for their failure to meet the test cannot be found, they must be discarded.
For a statement to be a proper scientific claim, it must be testable through experimentation. Claims that because of their structure could never be rejected through testing do not qualify as scientific statements. Notice that this restriction in no way implies that all scientific claims are true or that all nonscientific claims are false or meaningless. It merely notes that the goal of science is the understanding of physical reality and it limits the province of science to assertions that can be tested against physical reality.
To appreciate how modern scientific reasoning differs from other patterns of thought, it is useful to outline its procedures. One such outline, expressed as a list of instructions is:
1.Ask clear and precise questions.
2.Gather unambiguous and reliable data to answer those questions.
3.Examine the data to detect patterns.
4.Interpret the patterns; that is, formulate one or more hypotheses to explain the patterns. (This step cannot be carried out mechanically — it requires ingenuity, creativity, insight, and, occasionally, inspired guesswork.)
5.Doubt the hypotheses and attempt to disprove them. This is accomplished by generating otherwise unlikely predictions from the hypotheses and then testing, through experimentation, to see if the predictions come true. (It is this step that makes science different from other patterns of thought.)
6.If a hypothesis fails its test (i.e., if the predictions do not come true), modify, expand, or reject and replace the hypothesis and then generate and test new predictions.
7.Repeat, repeat, repeat ...
Although this pattern may seem commonplace (after all, it is precisely this pattern of reasoning that is used to determine why a car won't start or why a toaster won't toast or ...), it deserves considerable thought. In examining Mendel's work one should note how his actual research relates to this idealized description and you should recognize how his explanations were suggested by his data and how they were subjected to testing and confirmation.
Mendel's Monohybrid Crosses
To reduce ambiguity in his findings, Mendel first addressed the problem of heredity with very basic, very simple, and very clear questions:
1.What kinds and what numbers of progeny will be produced when parents differing only in one distinct trait (i.e., external attribute) are crossed?
2.What kinds and what numbers of offspring will be produced if the progeny of the original crosses are permitted to breed among themselves and to have progeny of their own?
In addition to asking clear questions, Mendel noted that, "The value and utility of any experiment are determined by the fitness of the material to the purpose for which it is used," and therefore he was careful to work with organisms that possessed attributes that were particularly appropriate for the study of heredity. Specifically, Mendel recognized that for genetic research to be successful, the researcher should be able to know the parentage of every experimental cross with certainty and should be able to differentiate easily among the various types of progeny that are produced. After considerable thought, he selected the garden pea for his subject. He believed them to be desirable for the following reasons.
1.Their flower structure was such that Mendel could be sure that accidental cross pollination by unknown plants would not occur. And, the flower structure also allowed Mendel to carry out the pollination himself so that he would be very certain about the actual parentage in all of his crosses. (Figure 2.1)
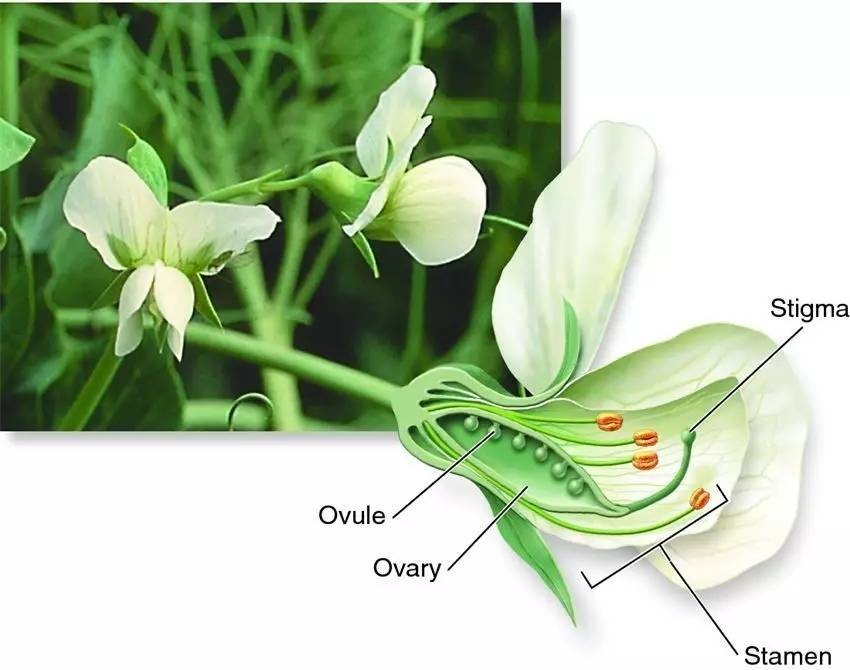
Figure 2.1. A cut-away illustration of the flower structure of the garden pea. Pollen is produced in the anthers and ova in the pistil. In peas, the anthers mature and release pollen while the flower is still in the bud stage — thus the pistil is normally protected from foreign pollen and the plants are self-fertilized. To carry out specific crosses, Mendel simply opened the bud, removed the anthers before they were mature, and applied to the pistil pollen taken from plants he had selected to be the male parent.
2.As a domesticated plant, they were available in a number of physically different, but interfertile forms. That is, Mendel was able to obtain and to cross pea plants that differed in very distinct and easily recognizable characteristics, such as seed shape or flower color. Furthermore, these attributes were known to be reliably heritable. (Figure 2.2)
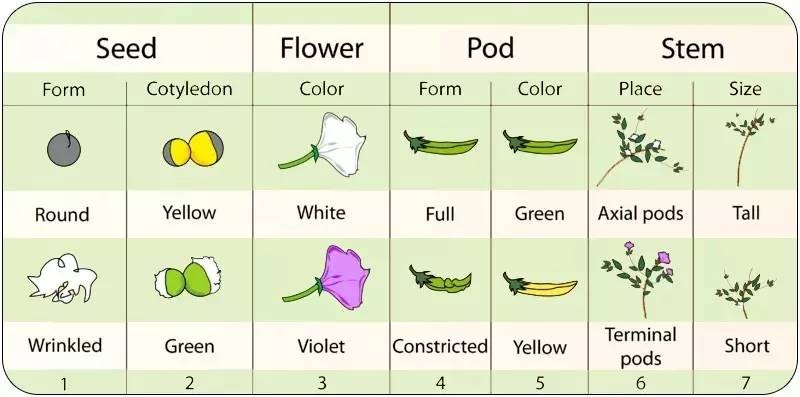
Figure 2.2. The seven different alternative sets of external attributes studied by Mendel.
3.They were relatively easy to maintain and cultivate and they showed no loss in fertility over several generations of breeding studies, so that Mendel was able to follow the patterns of inheritance for more than one generation.
Along with his careful selection of experimental subjects, Mendel designed and carried out his experimental procedures with precision.
1.He spent two years making sure that the peas he planned to use were True Breeding — that is, he allowed the plants to self fertilize so that he could verify that they would always produce progeny with precisely the same external attributes as themselves. By showing that his parental stocks always bred true he was able to ascertain that they carried only pure samples of the hereditary material.
2.He crossed plants that differed in only one distinct external attribute and he followed the crosses for more than one generation. To make sure that the data for different generations of progeny were kept separate, he used a notation where the parental generation was indicated with P, the first generation of progeny with F1, the second generation of progeny (i.e., those produced by the self fertilization of the F1 individuals) with F2, etc.
3.He used quantitative methods, performing many crosses and counting his results.
4.He performed Reciprocal Crosses — that is, whenever he performed crosses of red flowered and white flowered plants he made sure that in some of the crosses the red flowered plants provided the pollen and in other crosses the white flowered plants provided the pollen.
5.He analyzed his data quantitatively and discovered within each generation regular numerical patterns in the ratios of one progeny class to another. From these ratios he was able to develop detailed hypotheses regarding the apparent number and behavior of the physical particles that controlled the inheritance of characteristics.
6.He systematically checked his theories by performing new crosses to check new predictions generated by his hypotheses.
A final important influence on Mendel's success was his conceptual framework. He had been schooled in physics and mathematics, and thus he was able to interpret the quantitative patterns that appeared in his data. As you will see in the coming chapters, an appreciation of quantitative methods is very useful in the study of genetics.
Mendel's Findings
In his first experiments, Mendel collected data for two generations on several reciprocal crosses between pea plants that differed in only one characteristic — that is, he performed many Monohybrid Crosses. For example, he crossed plants that produced round seeds with those that produced wrinkled seeds. After each initial cross, he collected many F1 progeny and examined them to see if they resembled one or the other parent, or if they were transitional (i.e., showed attributes that were a mixture of those of both the parents). Then, he allowed the F1 progeny to self fertilize and to produce another generation, and he collected, analyzed, and counted the progeny from this second, F2, generation. His results are given in Table 2.1.
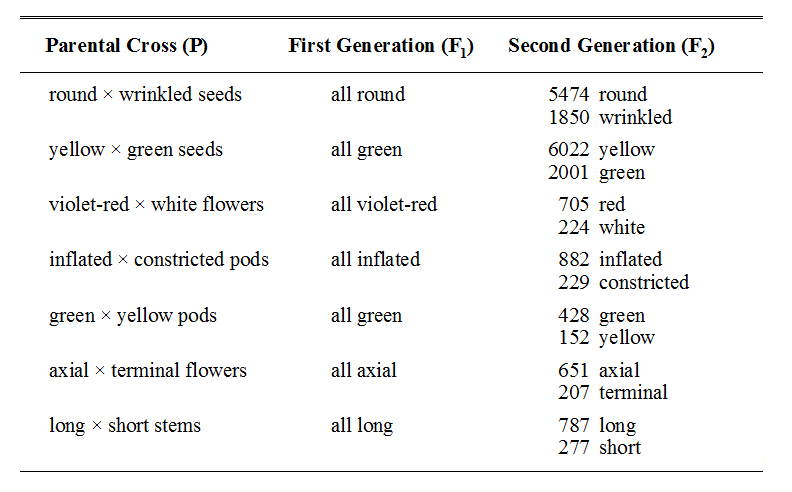
Table 2.1. A summary of Mendel's monohybrid crosses and their resulting sets of first and second generation progeny. In every cross, the first generation progeny all showed the external attribute of only one of the parents, but in the second generation both of the parental attributes appeared.
In examining his results, Mendel was immediately struck by the regularity of the qualitative and quantitative patterns shown in the progeny from all seven sets of crosses. In particular, he noted that:
1.In every cross, when two plants that differed in a particular external attribute were crossed, all of the F1 offspring possessed external attributes that were virtually identical with those of one and only one of the parents. Transitional (i.e., apparently mixed) attributes never occurred.
2.When the F1 plants were allowed to produce another generation of offspring (F2), both of the original parental external attributes appeared among the F2 progeny. That is, the external attribute that had disappeared in the F1 reappeared in some members of the F2. Furthermore, the two parental attributes always occurred in very regular proportions — three quarters of the F2 individuals showed the external attribute that had appeared in the F1, and one quarter showed the external attribute that had disappeared in the F1.
3.Reciprocal crosses produced equivalent results. That is, the results of the cross were the same regardless of which parent supplied the pollen and which the ova.
These observations are summarized in Figure 2.3.

Figure 2.3. Mendel found that in each of his reciprocal monohybrid crosses shows, all the F1 progeny resemble only one of the parental types, whereas the F2 progeny occur in a 3:1 ratio with the more common form being the same as that which appeared in the F1. This pattern was not affected by the original source (i.e., pollen or ova) of the attributes.
Mendel noticed immediately that these results were incompatible with a notion of blending inheritance. Although it might have been possible to explain away, under the theory of blending inheritance, the similarity of the F1 individuals to one of the parents (just as a mixture between a very dark red paint and a white paint may be so dark as to be indistinguishable from the original dark paint), it was impossible for blending inheritance to explain the reappearance in the F2 of the lost parental attribute. Under a theory of blending inheritance, this would be no more likely than the reappearance of a pint of pure white paint when poured from a gallon of mixed paint.
Instead, Mendel noted, these patterns could be more easily explained if heredity were controlled by the transmission of just a few physical particles from one generation to the next. And, he observed that the regular ratios he obtained suggested very strongly that each adult carried at most two different types of such particles for any given attribute (like flower color or seed shape) and that each parent transmitted precisely one copy of one of these particles to each offspring.
Mendel also made another very important observation — he noted that two plants might have identical external attributes yet possess fundamental differences in their hereditary material. For example, he observed that throughout his two years of preliminary testing every round seeded plant that he had allowed to self fertilize had bred true (i.e., produced only round seeded progeny), whereas all of the round seeded plants in the F1 from his cross of round by wrinkled failed to breed true, despite the fact that the F1 round seeded plants were physically indistinguishable from the parental P round seeded plants. This notion — that a logical and physical distinction must be made between an organism's external attributes and its internal hereditary material — is original with Mendel and it is fundamental to an understanding of genetics. You will encounter it over and over again throughout the text.
Mendel's reasoning can perhaps be better appreciated when it is expressed as a set of postulates:
1.Heredity is determined by Particulate Inheritance. That is, the external attributes of organisms are controlled by particles called (by Mendel) factors.
2.Hereditary particles occur, in any adult organism, in pairs (one pair for each external attribute to be controlled), so that, for a given attribute, adult organisms either carry all of one kind of factor or equal numbers of two different kinds of factors
3.When an organism produces gametes (eggs or sperm), a copy of only one member of each pair is placed into any given gamete. Furthermore, this placement is at random. Thus, if an adult organism carries matched pairs of factors for a given attribute, the organism will produce only gametes carrying that one kind of factor (i.e., the organism will be true breeding). However, if the organism carries unmatched pairs of factors, the organism will produce equal numbers of two different kinds of gametes — the first carrying one type of factor and the second the other.
4.The union of the gametes is random with respect to the hereditary factors that they are carrying.
5.When the gametes combine in fertilization, the newly produced individual begins life with a single pair of factors for each attribute (one member of the pair being supplied by each parent).
6.In affecting the outward appearance of the organism, some factors are Dominant and others are Recessive. Specifically, in a monohybrid cross the factor that controls the attribute that appears in the F1 is said to be dominant to the factor that controls the attribute that disappears in the F1. The factor that controls the attribute that disappears is said to be recessive. (This point will become clearer as we continue.)
If you examine these six postulates carefully, you will note that they fall into two distinct logical categories. The first five postulates give a set of rules governing the assortment of the hereditary factors, whereas the sixth gives a rule governing the relationship of an individual's factor makeup and its external appearance. The rules governing the assortment of factors have proved to be quite accurate and have not required much change or modification. Although the sixth rule is accurate in many cases, many situations have been found in which it has proved to be either too simplistic or even inaccurate. Some of these will be discussed in the next chapter.
Mendel's entire model can be illustrated with a generalized symbolic representation, with letters standing for factors such that an upper case letter indicates a dominant factor and a lower case letter indicates a recessive factor, as in Figure 2.4.

Figure 2.4. Mendel's theories can be represented symbolically, with the true-breeding parental organisms shown as possessing a matched pair of factors, whereas the non-true-breeding F1 organisms are shown as possessing an unmatched pair of factors. A symbolic representation shows that the 3:1 ratio of external attributes in the F2 is actually based on an underlying 1:2:1 ratio of organisms with different sets of factors.
You should examine Figure 2.4 carefully and you should compare it with Figure 2.3 and the list of Mendel's postulates to convince yourself of the accuracy of the representation. (The use of symbolic representation is widespread in genetics and you must acquire a thorough appreciation of this approach as quickly as possible.) Notice, for example, that the parental organisms are represented as AA and aa to indicate their true breeding status, and that as a result of having matched pairs of factors they can each produce only one kind of gamete. Since the F1 individuals are all produced by the union of one of each of these different gametes, the F1 are all indicated as having unmatched pairs of factors. According to the rule of dominance, the F1 are expected to have the same external appearance as the parental AA individuals, even though the F1 individuals have Aa sets of factors. And, because the F1 have Aa sets, they produce two different kinds of gametes in equal frequencies. Then, the random union of these different kinds of gametes yields F2 individuals, in a 1:2:1 ratio, with AA, Aa, and aa sets of factors. An explanation of why the random union of the F1 gametes should give this distribution in the F2 is given in the PUNNETT SQUARE of Figure 2.5. Punnett squares (named after their inventor — R. C. Punnett) are useful devices for calculating probability and frequency distributions (cf. Chapter 5).
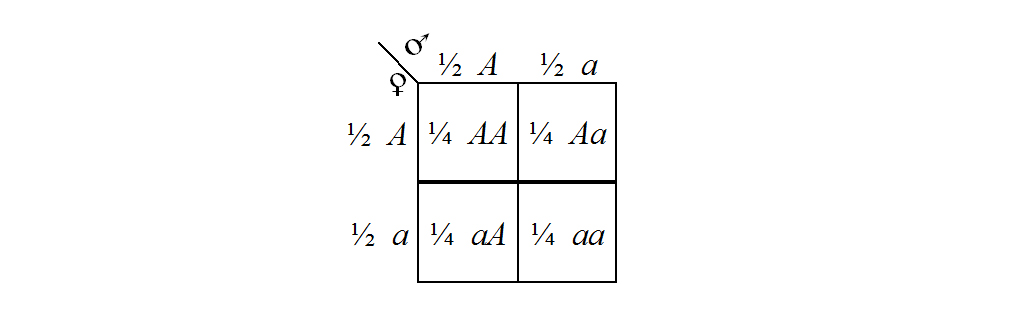
Figure 2.5. A Punnett square showing the systematic combination of all possible pairs of gametes produced by two individuals carrying an Aa set of hereditary factors. The fractions next to the gamete designations indicate the proportion of gametes carrying that factor, and the fractions next to the combination designations indicate the fraction of combinations carrying that pair of factors. Note that the combination Aa occurs in two of the cells in the square (Aa and aA are interchangeable) and that therefore the overall combinations and their associated fractions are 1/4 AA, 1/2 Aa, and 1/4 aa.
Mendel Tests His Model
Although his model of particulate inheritance was perfectly consistent with the data that he had obtained, Mendel recognized that such consistency in no way proves, nor even supports, the validity of a scientific theory. Indeed, any scientific theory (even an incorrect one) is expected to be consistent with the data from which it has been derived — the test of a theory comes in its ability to generate true predictions about new situations. To provide such a test, Mendel examined his model to generate some testable predictions. (Before going on, stop for a moment and look back over the model and its symbolic representation and see if you can generate some testable predictions that are not merely statements that the same results will be obtained if the experiment is repeated.)
In his examination, Mendel noted that in the cross of round seeded by wrinkled seeded plants, some round-seeded plants occurred in every generation: one of the parents had round seeds; all of the F1 were round; and 3/4 of the F2 were round. Furthermore, the round seeds of each generation looked exactly alike — there was no way to tell them apart by simple inspection. Despite this outward similarity, though, it appeared that in terms of factor makeup there were really two very different kinds of round seeded plants. According to the model, all of the parental round seeded plants carried only the factor for roundness, whereas all of the F1 round seeded plants carried, in equal numbers, factors for roundness and factors for wrinkledness. In the F2, the model showed that some of the round peas were like the parental round seeded plants and some were like the F1 round seeded plants. Specifically, the model indicated that 1/3 of the F2 round seeded plants should be like parental round seeded plants in terms of factor makeup and 2/3 should be like F1 round seeded plants. Finally, the model indicated that all wrinkled seeded plants from all generations in the cross always carried only factors for wrinkledness. (Examine the model carefully to convince yourself of the truth of these statements.)
There are two very interesting aspects to these claims drawn from the model. First, they are claims regarding the existence and behavior of entities that could not be detected by any methods available at the time, and therefore they deal with theoretical entities and cannot be tested directly. Second, although not subject to direct test, they can be tested indirectly through the derivation of predictions regarding results that can be observed. Specifically, if these claims regarding factor makeup (and the rest of the model) are correct, then it would be possible to predict with precision the types and frequencies of progeny to be expected from certain crosses. Thus, Mendel generated and tested two predictions:
1.If any F1 round seeded plant is crossed with any wrinkled seeded plant, half of the progeny produced will be round, half wrinkled.
2.If many of the F2 round seeded plants are allowed to self fertilize, 1/3 of them should breed true (i.e., produce only round seeded progeny), whereas 2/3 of them should produce both round and wrinkled progeny in a 3:1 ratio.
These predictions were excellent tests of the model because they were clear and precise and because they were unlikely to prove true unless the model was correct. (As an exercise, you should examine the model and then diagram the crosses of both predictions to see why they do follow from the model.)
Mendel carried out the appropriate crosses and in both cases the predictions came true. Because these predictions regarding progeny frequency were derived from Mendel's hypothesis regarding the existence and behavior of unseen factors, the fulfillment of the predictions strengthened Mendel's belief in the validity of his hypothesis. The generation (and testing) of predictions with observable results from hypotheses involving entities that cannot easily be observed directly is common in all genetic research. Therefore, you should make sure that you understand the validity of this reasoning, as its mastery is essential for the mastery of genetics.
Mendel's Dihybrid Crosses
Mendel recognized that his model provided neither a simple nor a single explanation for what would happen in a cross in which the parents differed in two traits, such as seed color and seed shape. This type of cross is known as a Dihybrid Cross. Specifically, he noted that in a dihybrid cross the distribution of one pair of factors into gametes might or might not be influenced by the distribution of another pair of factors, and that the data from monohybrid crosses could provide no unambiguous insights into this issue. To determine how the factors would actually assort in a dihybrid cross, Mendel crossed plants that had seeds that were both round and yellow with plants that had seeds that were both wrinkled and green.
From his results with monohybrid crosses, Mendel knew that although the F1 would show only the dominant attributes, it would actually be carrying both round and wrinkled and both yellow and green factors. Thus, he knew that half of the gametes produced by the F1 would carry the factor for roundness and half the factor for wrinkledness and that similarly, half of the gametes would carry the factor for yellowness and half the factor for greenness. But, the results of the monohybrid crosses provided no information that Mendel could use to decide whether the assortment of round and wrinkled factors would be in any way influenced by the assortment of yellow and green factors.
However, Mendel realized that according to the laws of probability theory (cf. Chapter 5) there were only three different possible relationships for the assortment of the two sets of factors, and that therefore there were only three different possible hypotheses that could explain how the F1 might make gametes. Furthermore, Mendel noted that each of these three hypotheses led to a distinctly different prediction regarding the makeup of the F2. Thus, Mendel realized that he could decide which of these hypotheses was in fact true by comparing the actual results obtained in the F2 with the different predictions of the three hypotheses. (This type of experiment in which the results of a single experiment are compared simultaneously with the competing predictions of competing hypotheses is now known as a Crucial Experiment.) Specifically, Mendel noted that:
1.The distribution of the two sets of factors might be completely dependent (in the probabilistic sense), in which case the F1 would make only two different kinds of gametes and as a result the F2 would be expected to occur as only two immediately distinguishable types (round yellow and wrinkled green) and they should occur in a 3:1 ratio.
2.The distribution of the two sets of factors might be completely independent (in the probabilistic sense), in which case the F1 would make four different kinds of gametes, in equal frequency, and as a result the F2 would be expected to occur as four immediately distinguishable types (round yellow, round green, wrinkled yellow, and wrinkled green) and these should occur in a 9:3:3:1 ratio.
3.The distribution of the two sets of factors might show partial dependence (in the probabilistic sense), in which case the F1 would make four different kinds of gametes, in unequal frequency, and as a result the F2 would be expected to occur as four immediately distinguishable types but that these would occur in ratios different from 9:3:3:1.
To see how these different predictions derive from these different hypotheses, let
R = the factor for roundness
r = the factor for wrinkledness
Y = the factor for yellowness
y = the factor for greenness
Then the problem associated with crossing true breeding round yellow by true breeding wrinkled green can be represented as follows.

stuff
Consider how this derives from the model. The parental plants each place one member of each pair of factors into every gamete. There is no question regarding the factor makeup of the parental gametes, since they carry only one kind of factor for each external attribute. Then, these parental gametes combine and produce only one kind of F1 individual, RrYy. According to the rule of dominance, this individual will show the round and yellow external attributes. When the F1 individuals make gametes, the model from the monohybrid crosses states that each gamete will contain one member of the R/r pair and one member of the Y/y pair. However, the model makes no specific prediction regarding the types of gametes to be produced by the F1, when both sets of factors are considered together. Indeed, the three different predictions that can be made are all consistent with the basic model. We will now consider these predictions in greater detail.
Prediction 1, Complete Dependence
If the assortment of the factors in the production of gametes by the F1 is completely dependent (that is, if the assortment of the Y/y factors follows exactly the assortment of the R/r factors), then the Y factor will always "stick to" the R factor and the y factor will "stick" to the r factor. (Why predict that R might stick to Y and r to y? Because they came in together in the parental gametes and the model for the monohybrid cross provides no way of knowing whether or not factors for different traits might be physically attached to each other in the gamete.) Thus, in this case the F1 would produce only two kinds of gametes (RY and ry) in equal frequencies. A Punnett square, Figure 2.6, shows what would then be expected in the F2.

Figure 2.6. A Punnett square showing the predicted results for the F2, if the assortment of one pair of factors is completely dependent upon the assortment of another pair of factors.
From Figure 2.6, we see that, in terms of factor makeup, the F2 would contain 1/4 RRYY, 1/2 RrYy, and 1/4 rryy individuals. That is, the F2 would contain three different types occurring in a 1:2:1 ratio. However, because of dominance, both the RRYY and the RrYy individuals would be round and yellow. Thus, under the assumption of complete dependence, it is predicted that the F2 would occur as only two immediately distinguishable types (round yellow and wrinkled green) and these would occur in a 3:1 ratio.
Prediction 2, Complete Independence
If the assortment of the factors in the production of gametes by the F1 is completely independent (that is, if the assortment of the Y/y factors into particular gametes is in no way affected by the assortment of the R/r factors such as would be expected if the different pairs of factors were not physically attached to each other), then half of all the R carrying gametes would have the Y factor and half would have the y factor and similarly for the r carrying gametes. Thus, in this case the F1 would produce four different kinds of gametes (RY, Ry, rY, and ry) in equal frequencies. Again, a Punnett square, Figure 2.7, shows what would be expected in the F2.

Figure 2.7. A Punnett square showing the predicted results for the F2, if the assortment of one pair of factors is completely independent of the assortment of another pair of factors
If you go through the four-by-four Punnett square of Figure 2.7 and count up all the different types (and you should), you will see that, in terms of factor makeup, the F2 would contain nine different types (RRYY, RRYy, RRyy, RrYY, RrYy, Rryy, rrYY, rrYy, and rryy) and that these would occur in a 1:2:1:2:4:2:1:2:1 ratio. However, because of dominance these nine would collapse into only four immediately distinguishable types. Specifically, the RRYY, RRYy, RrYY, and RrYy, individuals would all be round yellow, the RRyy and Rryy individuals would both be round green, the rrYY and rrYy individuals would both be wrinkled yellow, and only the rryy individuals would be wrinkled green. Thus, under this prediction, the F2 would occur as only four immediately distinguishable types (round yellow, round green, wrinkled yellow, and wrinkled green) and these would occur in a 9:3:3:1 ratio. (You should consider this square carefully and convince yourself of the truth of these claims.)
Prediction 3, Partial Dependence
If the assortment of the factors in the production of gametes by the F1 is partially dependent (that is, if the assortment of the Y/y factors is sometimes affected and sometimes not affected by the assortment of the R/r factors such as would happen if the factors were usually attached to each other but somehow occasionally became unattached), then often the Y factor would stick to the R factor, but sometimes it wouldn't. This would cause the F1 to produce four different kinds of gametes in unequal frequencies. For example, in one case of partial dependence, the F1 might produce 3/8 RY, 1/8 Ry, 1/8 rY, and 3/8 ry gametes. (You, should draw your own four-by-four Punnett square and determine what frequency of different immediately distinguishable types of progeny would occur in the F2 under this example. If you do it correctly, you will see that it does not give a 9:3:3:1 ratio.)
Mendel's Results for a Dihybrid Cross
To determine which of these possibilities was in fact the case, Mendel performed a cross in which one true breeding parent had round and yellow seeds and the other true breeding parent had wrinkled and green seeds. The results of that cross are given in Table 2.2.

Table 2.2. A summary of the results of Mendel's dihybrid cross. As in the monohybrid crosses, only the dominant traits appeared in the F1, whereas both the dominant and recessive traits appeared in the F2. However, the F2 contained some round & green and some wrinkled & yellow plants — combinations not found in the parents.
The results, almost a perfect 9:3:3:1 ratio, were very close to the predictions of complete statistical independence. Therefore, it appeared to Mendel that the hypothesis of complete independence was correct and that the hypotheses of complete dependence and partial dependence were false. To check the validity of this idea, Mendel performed some additional dihybrid crosses and even one Trihybrid Cross. When all of these gave results consistent with independent assortment, Mendel extended his model to include the findings from the dihybrid crosses. This can be indicated by adding a seventh postulate to Mendel's model:
7.The assortment of one pair of hereditary factors into gametes is independent of the assortment of any other pair.
You should compare this new postulate with the other six and note that this seventh postulate is an extension to the rules governing the assortment of hereditary factors. Postulate six is still the only rule governing the relationship of an individual's factor makeup and its outward appearance.
NOTE: Although Mendel's work in the derivation of this last postulate regarding independent assortment was perfectly correct as far as it went, later work has shown that independent assortment is true for some pairs of factors and not for others. Thus, you should be prepared to adjust your understanding of the rules governing the assortment of different pairs of hereditary factors when we encounter the implications of that later work in Chapters 6, 7, and 8.
Mendel's Tests of Independent Assortment
As before, Mendel realized that he would have to generate and test some predictions regarding new situations before he should feel confident regarding the truth of this hypothesis. He began by developing a symbolic notation to represent the results of the dihybrid cross and then examining it to generate predictions (Figure 8).

Figure 2.8. A symbolic representation of the results of Mendel's dihybrid cross. According to the model the parental plants can each produce only one kind of gamete, whereas the F1 plants produce four different kinds of gametes in equal frequency. The F2 plants occur as four different types when classified by their external attributes, but as nine different types when classified by their factor makeup.
In his examination, Mendel noted first that the model required that the F1 plants produce four different kinds of gametes in equal frequency. And, he noted that the model suggested that although there were only four different kinds of plants in the F2, when classified according to their outward appearance, in actuality there were nine different kinds when classified according to their factor makeup. As before, Mendel used these claims regarding undetectable (by Mendel, anyway) entities to make predictions regarding progeny types and frequencies from specific crosses and selfings (i.e., self fertilizations):
1.If any F1 round and yellow plant is crossed with any wrinkled and green plant, four types of progeny (round and yellow, round and green, wrinkled and yellow, and wrinkled and green) should be produced in equal frequencies.
2.If all of the F2 plants are allowed to self, some of them will breed true for both characters, some for only one character, and some for neither character. Specifically, if only the round and yellow members of the F2 are considered, 1/9 of them should breed true for both characters, 2/9 should breed true for roundness but not for yellowness, 2/9 should breed true for yellowness but not for roundness, and 4/9 should not breed true for either character. Similarly, if only the round and green members of the F2 are considered, 1/3 of them should breed true for both characters and 2/3 should breed true only for greenness. Of the wrinkled and yellow members of the F2, 1/3 should breed true for both characters and 2/3 should breed true only for wrinkledness. Finally, the wrinkled and green members of the F2 should all breed true for both characters.
Mendel carried out the appropriate crosses and selfings and in every case the predictions came true, greatly strengthening Mendel's belief in his model. (You should examine Figures 2.7 and 2.8 carefully to see why these predictions follow directly from Mendel's overall model and the assumption of independent assortment of different pairs of factors.)
Mendel's Laws
To make the logical foundation of Mendel's model readily apparent, we have discussed Mendel's model as comprising seven postulates. However, many others have summarized his work as two laws. Because these laws have become part of the terminology of the study of heredity, we offer them here so that you will be familiar with them if you encounter them in other works. You should note that neither these laws nor our seven postulates appear specifically in Mendel's own paper.
1.Law of Random Segregation: During gametogenesis, pairs of hereditary factors segregate randomly into gametes.
2.Law of Independent Assortment: The segregation of one pair of factors is independent of the assortment of other pairs of factors.
Mendel's Ideas in a Modern Vocabulary
To facilitate our further discussion of Mendelian heredity, we will now pause for a moment to establish a modern vocabulary. You should bear in mind that, like the vocabulary of any language, these words were developed over time, with occasional shifts and additions in meaning. (At first this may seem bothersome to you, but it shouldn't. At least it shouldn't any more than you find it bothersome that standard English words tend to have several meanings. For example, consider the word "family". What does "family" mean? Of course you know, but suppose I ask you if you should consider your second cousin to be a member of your family. The answer to this clearly depends upon the specific meaning of "family" that is intended. You will find that a similar situation obtains with the technical vocabulary of heredity. While all of the words do have precise definitions, they also have variations in meaning so that you must pay attention to their contextual usages as well.)
To begin, the particles of inheritance — the Mendelian factors — are now known as Genes. The overall science of heredity is Genetics and the specialized branch of genetics that deals with the ways in which hereditary material is passed from parent to offspring is known as Transmission Genetics. In the vocabulary of genetics, the word gene is particularly subject to variations in meaning, since sometimes we may use it in a general way such as, a gene for seed color in peas, in which case we would mean either the factor for yellowness or the factor for greenness. Or, we may say, the gene for yellow, in which case we mean only the factor for yellowness. Additionally, as our understanding of the chemical nature and action of the hereditary material has increased, so has our definition of gene become more refined. Thus, you should be prepared to adjust your mental definition of gene as we discuss these refinements in later chapters.
To restrict ourselves to particular factors, we speak of Alleles. The term allele refers to a specific, alternate form of the hereditary factors governing a particular trait. For example, the genes for seed color can be specified as the allele for yellowness and the allele for greenness. Also, we speak of hereditary factors as being Allelic to each other when they can occur together as pairs. That is, the factor for roundness is allelic to the factor for wrinkledness, but the factor for roundness is not allelic to the factor for yellowness. Thus, in Mendel's studies round and wrinkled were the alleles for seed shape, yellow and green the alleles for seed color, etc.
In the previous chapter we noted that chromosomes are the carriers of the hereditary material. It is also true that the alleles of a given gene are always carried at a particular place on a particular pair of homologous chromosomes. We can refer to this place as the gene's Locus (which is just the Latin word for position). The notion of locus is also very useful for clarifying the allelic relationship between factors. Specifically, the factor for roundness is allelic to that for wrinkledness because normally they both occur at the same locus. However, the factor for yellowness occurs at a different locus so it is not allelic to the factors for roundness or wrinkledness. (For a more refined consideration of this aspect of allelism, see the discussion of the complementation test in Supplement 4.1 and in Chapter 7.)
If we now examine Mendel's round-by-wrinkled cross and consider both the plants' outward appearance and their inner genetic makeup, we see the need for some additional terms:
Notice that a plant can either carry two of the same allele or two different alleles for a given locus. If an organism is carrying two identical alleles at a particular locus, we say that the organism is Homozygous at that locus, and we may refer to the homozygous individual as a Homozygote. If the organism is carrying two different alleles at a given locus, we say that the individual is Heterozygous, and we refer to the individual as a Heterozygote. We can also be more specific and refer to an individual as being, for example, homozygous dominant, or even as being homozygous round.
Notice also that the plants in this cross have only two different types of outward appearance (round or wrinkled), but they can have any of three different possible sets of alleles (RR, Rr, or rr). To distinguish between these, we refer to the outward appearance as the organism's Phenotype and its actual genetic makeup as its Genotype. Recall that one of Mendel's major contributions was that he recognized that plants could have the same outward appearance, yet still be different in their factor makeup — that is, without using the modern terms, Mendel distinguished between a plant's phenotype and its genotype.
Sometimes if you know a plant's phenotype you can automatically determine what its genotype must be, but other times you cannot. For example, a plant with the wrinkled phenotype must have the genotype rr, because this is the only genotype that gives the wrinkled phenotype. However, if you know that a plant is round you do not know its exact genotype because both the RR and the Rr genotypes give the round phenotype. But, if a plant is round, you do know part of its genotype — that is, you know that it must be carrying at least one allele for roundness. Therefore, you could symbolize its genotype as R to indicate that one allele is known to be R but that the other allele is unknown. Generally, organisms with the recessive phenotype must have the homozygous recessive genotype, whereas organisms with the dominant phenotype may have either the homozygous dominant or the heterozygous genotype. Thus, we can now further refine our definitions of dominant and recessive so that we call an allele recessive if it produces its phenotype only when it is carried homozygously and we call an allele dominant if it produces its phenotype when it is carried homozygously or heterozygously.
Since, by definition, RR and Rr are identical in their outward appearance, you might be wondering how in fact you could ever tell them apart. The answer is, you cross a plant showing the dominant phenotype with a homozygous recessive plant. If the round plant is actually RR, then all of the progeny from the cross will be Rr and therefore round. On the other hand, if the plant is actually Rr, half of the progeny will be Rr and round but the other half will be rr and wrinkled. (If you are not sure you follow this, diagram the two possibilities to see why this works.) This type of cross where an organism of unknown genotype is crossed with a recessive homozygote is known as a Test Cross. (Recall that Mendel used test crossing as part of his follow-up analyses in both his monohybrid and dihybrid crosses.)
Returning to the round by wrinkled cross illustrated above, in the F2 there is a 3:1 Phenotypic Ratio, and that is produced by the rule of dominance acting on an underlying 1:2:1 Genotypic Ratio. You should understand these distinctions between genotype and phenotype and between genotypic and phenotypic ratios very clearly, as many of the concepts of modern genetics depend upon them.
Finally, to test your understanding of these new vocabulary terms you should reread the discussion of Mendel's own work and try to convert it into the modern terms. For example, a translation of the law of independent assortment might read, the segregation of alleles at any one locus is independent of the assortment of alleles at any other locus.
Summary and Overview
In one brilliant experimental sequence, Gregor Mendel provided not only the foundation but nearly the entire structure of modern transmission genetics. Mendel's most important and most enduring contributions were his observations that (a) inheritance is particulate; (b) the hereditary particles are carried in pairs in adults and that the members of these pairs of particles segregate from each other during gametogenesis so that they are carried singly in gametes; and (c) there is a fundamental distinction between an organism's genotype and its phenotype.
Despite the astounding accuracy and clarity of Mendel's work (a modern reader is struck with the depth of Mendel's understanding), his findings went unrecognized and neglected for 34 years following its publication. Indeed, Mendel died, probably believing that his studies on peas had been a waste of time, before the importance of his work was recognized. Why? How could such important findings be so totally ignored? Perhaps because biological science at that time could provide no evidence for any real, physical units within cells that might be the equivalent of Mendel's hereditary factors. Chromosomes had not yet been studied, meiosis not yet described, and without this basic knowledge it may have seemed that Mendel's detailed quantitative theories were mere numerology.
ESP Picks from Around the Web (updated 28 JUL 2024 )
Old Science

Weird Science

Treating Disease with Fecal Transplantation
Fossils of miniature humans (hobbits) discovered in Indonesia
Paleontology

Dinosaur tail, complete with feathers, found preserved in amber.
Astronomy

Mysterious fast radio burst (FRB) detected in the distant universe.
Big Data & Informatics

Big Data: Buzzword or Big Deal?
Hacking the genome: Identifying anonymized human subjects using publicly available data.