MENU
The Electronic Scholarly Publishing Project: Providing world-wide, free access to classic scientific papers and other scholarly materials, since 1993.
More About: ESP | OUR CONTENT | THIS WEBSITE | WHAT'S NEW | WHAT'S HOT
ESP Essays 14 Jul 2025 Updated:
Mendel's Work, II
Monohybrid Crosses
Like begets like, more or less. This basic fact of heredity has been known since ancient times. However, the actual mechanisms of heredity, indeed, even the mathematical patterns of heredity, were completely unknown until Gregor Mendel did his breakthough work. When he published his findings in 1866, the scientific failed to recognize their significance and the work was largely ignored, until it was rediscovered in 1900. many recognized the huge potential in his findings, triggering an explosion of work that, in just two decades, laid the complete foundation of our modern understanding of genetics.
Mendel's Monohybrid Crosses

Gregor Mendel
To reduce ambiguity in his findings, Mendel first addressed the problem of heredity with very basic, very simple, and very clear questions:
1.What kinds and what numbers of progeny will be produced when parents differing only in one distinct trait (i.e., external attribute) are crossed?
2.What kinds and what numbers of offspring will be produced if the progeny of the original crosses are permitted to breed among themselves and to have progeny of their own?
In addition to asking clear questions, Mendel noted that, "The value and utility of any experiment are determined by the fitness of the material to the purpose for which it is used," and therefore he was careful to work with organisms that possessed attributes that were particularly appropriate for the study of heredity. Specifically, Mendel recognized that for genetic research to be successful, the researcher should be able to know the parentage of every experimental cross with certainty and should be able to differentiate easily among the various types of progeny that are produced. After considerable thought, he selected the garden pea for his subject. He believed them to be desirable for the following reasons.
1.Their flower structure was such that Mendel could be sure that accidental cross pollination by unknown plants would not occur. And, the flower structure also allowed Mendel to carry out the pollination himself so that he would be very certain about the actual parentage in all of his crosses. (Figure 1)
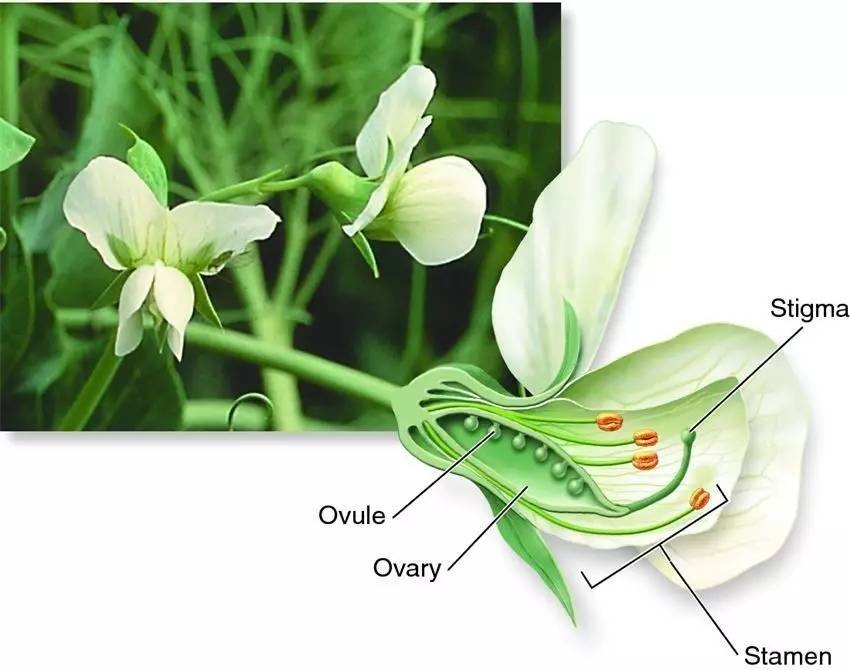
Figure 1. A cut-away illustration of the flower structure of the garden pea. Pollen is produced in the anthers and ova in the pistil. In peas, the anthers mature and release pollen while the flower is still in the bud stage — thus the pistil is normally protected from foreign pollen and the plants are self-fertilized. To carry out specific crosses, Mendel simply opened the bud, removed the anthers before they were mature, and applied to the pistil pollen taken from plants he had selected to be the male parent.
2.As a domesticated plant, they were available in a number of physically different, but interfertile forms. That is, Mendel was able to obtain and to cross pea plants that differed in very distinct and easily recognizable characteristics, such as seed shape or flower color. Furthermore, these attributes were known to be reliably heritable. (Figure 2)
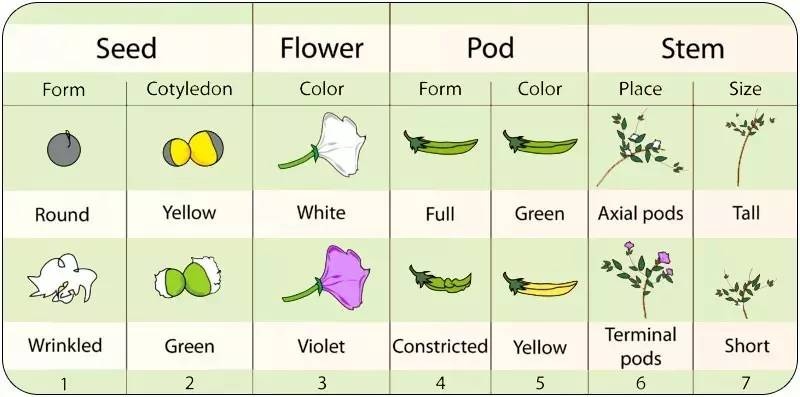
Figure 2. The seven different alternative sets of external attributes studied by Mendel.
3.They were relatively easy to maintain and cultivate and they showed no loss in fertility over several generations of breeding studies, so that Mendel was able to follow the patterns of inheritance for more than one generation.
Along with his careful selection of experimental subjects, Mendel designed and carried out his experimental procedures with precision.
1.He spent two years making sure that the peas he planned to use were TRUE BREEDING — that is, he allowed the plants to self fertilize so that he could verify that they would always produce progeny with precisely the same external attributes as themselves. By showing that his parental stocks always bred true he was able to ascertain that they carried only pure samples of the hereditary material.
2.He crossed plants that differed in only one distinct external attribute and he followed the crosses for more than one generation. To make sure that the data for different generations of progeny were kept separate, he used a notation where the parental generation was indicated with P, the first generation of progeny with F1, the second generation of progeny (i.e., those produced by the self fertilization of the F1 individuals) with F2, etc.
3.He used quantitative methods, performing many crosses and counting his results.
4.He performed RECIPROCAL CROSSES — that is, whenever he performed crosses of red flowered and white flowered plants he made sure that in some of the crosses the red flowered plants provided the pollen and in other crosses the white flowered plants provided the pollen.
5.He analyzed his data quantitatively and discovered within each generation regular numerical patterns in the ratios of one progeny class to another. From these ratios he was able to develop detailed hypotheses regarding the apparent number and behavior of the physical particles that controlled the inheritance of characteristics.
6.He systematically checked his theories by performing new crosses to check new predictions generated by his hypotheses.
A final important influence on Mendel's success was his conceptual framework. He had been schooled in physics and mathematics, and thus he was able to interpret the quantitative patterns that appeared in his data. As you will see in the coming chapters, an appreciation of quantitative methods is very useful in the study of genetics.
Mendel's Findings
In his first experiments, Mendel collected data for two generations on several reciprocal crosses between pea plants that differed in only one characteristic — that is, he performed many MONOHYBRID CROSSES. For example, he crossed plants that produced round seeds with those that produced wrinkled seeds. After each initial cross, he collected many F1 progeny and examined them to see if they resembled one or the other parent, or if they were transitional (i.e., showed attributes that were a mixture of those of both the parents). Then, he allowed the F1 progeny to self fertilize and to produce another generation, and he collected, analyzed, and counted the progeny from this second, F2, generation. His results are given in Table 1.
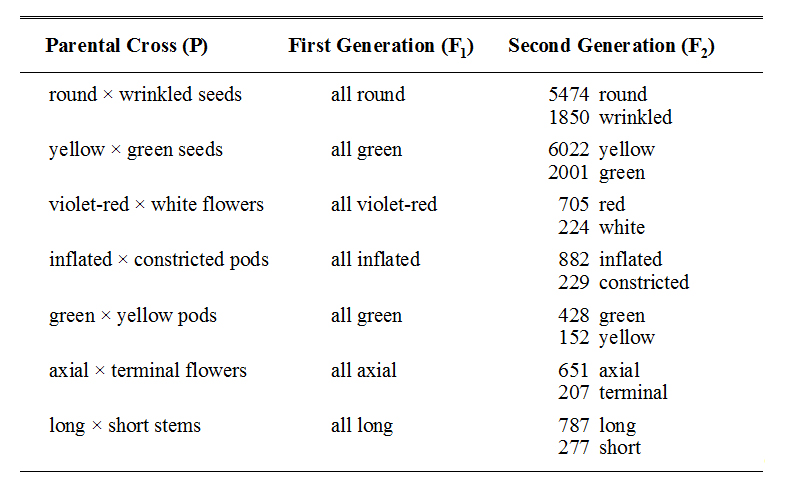
Table 1. A summary of Mendel's monohybrid crosses and their resulting sets of first and second generation progeny. In every cross, the first generation progeny all showed the external attribute of only one of the parents, but in the second generation both of the parental attributes appeared.
In examining his results, Mendel was immediately struck by the regularity of the qualitative and quantitative patterns shown in the progeny from all seven sets of crosses. In particular, he noted that:
1.In every cross, when two plants that differed in a particular external attribute were crossed, all of the F1 offspring possessed external attributes that were virtually identical with those of one and only one of the parents. Transitional (i.e., apparently mixed) attributes never occurred.
2.When the F1 plants were allowed to produce another generation of offspring (F2), both of the original parental external attributes appeared among the F2 progeny. That is, the external attribute that had disappeared in the F1 reappeared in some members of the F2. Furthermore, the two parental attributes always occurred in very regular proportions — three quarters of the F2 individuals showed the external attribute that had appeared in the F1, and one quarter showed the external attribute that had disappeared in the F1.
3.Reciprocal crosses produced equivalent results. That is, the results of the cross were the same regardless of which parent supplied the pollen and which the ova.
These observations are summarized in Figure 3.

Figure 3. Mendel found that in each of his reciprocal monohybrid crosses shows, all the F1 progeny resemble only one of the parental types, whereas the F2 progeny occur in a 3:1 ratio with the more common form being the same as that which appeared in the F1. This pattern was not affected by the original source (i.e., pollen or ova) of the attributes
Mendel noticed immediately that these results were incompatible with a notion of blending inheritance. Although it might have been possible to explain away, under the theory of blending inheritance, the similarity of the F1 individuals to one of the parents (just as a mixture between a very dark red paint and a white paint may be so dark as to be indistinguishable from the original dark paint), it was impossible for blending inheritance to explain the reappearance in the F2 of the lost parental attribute. Under a theory of blending inheritance, this would be no more likely than the reappearance of a pint of pure white paint when poured from a gallon of mixed paint.
Instead, Mendel noted, these patterns could be more easily explained if heredity were controlled by the transmission of just a few physical particles from one generation to the next. And, he observed that the regular ratios he obtained suggested very strongly that each adult carried at most two different types of such particles for any given attribute (like flower color or seed shape) and that each parent transmitted precisely one copy of one of these particles to each offspring.
Mendel also made another very important observation — he noted that two plants might have identical external attributes yet possess fundamental differences in their hereditary material. For example, he observed that throughout his two years of preliminary testing every round seeded plant that he had allowed to self fertilize had bred true (i.e., produced only round seeded progeny), whereas all of the round seeded plants in the F1 from his cross of round by wrinkled failed to breed true, despite the fact that the F1 round seeded plants were physically indistinguishable from the parental P round seeded plants. This notion — that a logical and physical distinction must be made between an organism's external attributes and its internal hereditary material — is original with Mendel and it is fundamental to an understanding of genetics. You will encounter it over and over again throughout the text.
Mendel's reasoning can perhaps be better appreciated when it is expressed as a set of postulates:
1.Heredity is determined by PARTICULATE INHERITANCE. That is, the external attributes of organisms are controlled by particles called (by Mendel) factors.
2.Hereditary particles occur, in any adult organism, in pairs (one pair for each external attribute to be controlled), so that, for a given attribute, adult organisms either carry all of one kind of factor or equal numbers of two different kinds of factors
3.When an organism produces gametes (eggs or sperm), a copy of only one member of each pair is placed into any given gamete. Furthermore, this placement is at random. Thus, if an adult organism carries matched pairs of factors for a given attribute, the organism will produce only gametes carrying that one kind of factor (i.e., the organism will be true breeding). However, if the organism carries unmatched pairs of factors, the organism will produce equal numbers of two different kinds of gametes — the first carrying one type of factor and the second the other.
4.The union of the gametes is random with respect to the hereditary factors that they are carrying.
5.When the gametes combine in fertilization, the newly produced individual begins life with a single pair of factors for each attribute (one member of the pair being supplied by each parent).
6.In affecting the outward appearance of the organism, some factors are DOMINANT and others are RECESSIVE. Specifically, in a monohybrid cross the factor that controls the attribute that appears in the F1 is said to be dominant to the factor that controls the attribute that disappears in the F1. The factor that controls the attribute that disappears is said to be recessive. (This point will become clearer as we continue.)
If you examine these six postulates carefully, you will note that they fall into two distinct logical categories. The first five postulates give a set of rules governing the assortment of the hereditary factors, whereas the sixth gives a rule governing the relationship of an individual's factor makeup and its external appearance. The rules governing the assortment of factors have proved to be quite accurate and have not required much change or modification. Although the sixth rule is accurate in many cases, many situations have been found in which it has proved to be either too simplistic or even inaccurate. Some of these will be discussed in the next chapter.
Mendel's entire model can be illustrated with a generalized symbolic representation, with letters standing for factors such that an upper case letter indicates a dominant factor and a lower case letter indicates a recessive factor, as in Figure 4.

Figure 4. Mendel's theories can be represented symbolically, with the true-breeding parental organisms shown as possessing a matched pair of factors, whereas the non-true-breeding F1 organisms are shown as possessing an unmatched pair of factors. A symbolic representation shows that the 3:1 ratio of external attributes in the F2 is actually based on an underlying 1:2:1 ratio of organisms with different sets of factors.
You should examine Figure 4 carefully and you should compare it with Figure 3 and the list of Mendel's postulates to convince yourself of the accuracy of the representation. (The use of symbolic representation is widespread in genetics and you must acquire a thorough appreciation of this approach as quickly as possible.) Notice, for example, that the parental organisms are represented as AA and aa to indicate their true breeding status, and that as a result of having matched pairs of factors they can each produce only one kind of gamete. Since the F1 individuals are all produced by the union of one of each of these different gametes, the F1 are all indicated as having unmatched pairs of factors. According to the rule of dominance, the F1 are expected to have the same external appearance as the parental AA individuals, even though the F1 individuals have Aa sets of factors. And, because the F1 have Aa sets, they produce two different kinds of gametes in equal frequencies. Then, the random union of these different kinds of gametes yields F2 individuals, in a 1:2:1 ratio, with AA, Aa, and aa sets of factors. An explanation of why the random union of the F1 gametes should give this distribution in the F2 is given in the PUNNETT SQUARE of Figure 5. Punnett squares (named after their inventor — R. C. Punnett) are useful devices for calculating probability and frequency distributions (cf. Chapter 5).
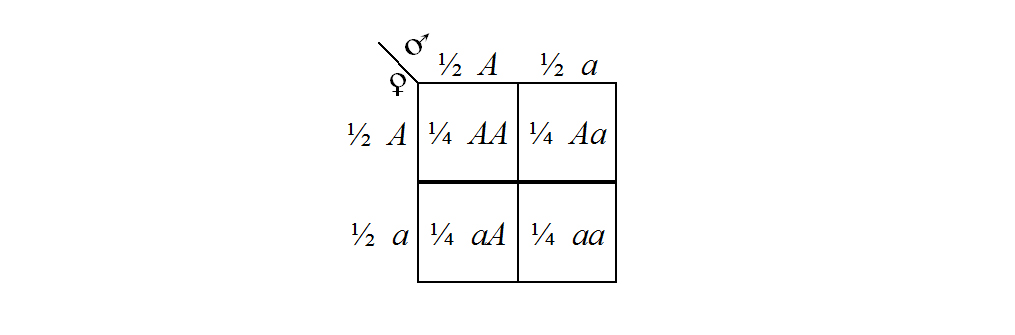
Figure 5. A Punnett square showing the systematic combination of all possible pairs of gametes produced by two individuals carrying an Aa set of hereditary factors. The fractions next to the gamete designations indicate the proportion of gametes carrying that factor, and the fractions next to the combination designations indicate the fraction of combinations carrying that pair of factors. Note that the combination Aa occurs in two of the cells in the square (Aa and aA are interchangeable) and that therefore the overall combinations and their associated fractions are 1/4 AA, 1/2 Aa, and 1/4 aa.
Mendel's Tests of his Model
Although his model of particulate inheritance was perfectly consistent with the data that he had obtained, Mendel recognized that such consistency in no way proves, nor even supports, the validity of a scientific theory. Indeed, any scientific theory (even an incorrect one) is expected to be consistent with the data from which it has been derived — the test of a theory comes in its ability to generate true predictions about new situations. To provide such a test, Mendel examined his model to generate some testable predictions. (Before going on, stop for a moment and look back over the model and its symbolic representation and see if you can generate some testable predictions that are not merely statements that the same results will be obtained if the experiment is repeated.)
In his examination, Mendel noted that in the cross of round seeded by wrinkled seeded plants, some round-seeded plants occurred in every generation: one of the parents had round seeds; all of the F1 were round; and 3/4 of the F2 were round. Furthermore, the round seeds of each generation looked exactly alike — there was no way to tell them apart by simple inspection. Despite this outward similarity, though, it appeared that in terms of factor makeup there were really two very different kinds of round seeded plants. According to the model, all of the parental round seeded plants carried only the factor for roundness, whereas all of the F1 round seeded plants carried, in equal numbers, factors for roundness and factors for wrinkledness. In the F2, the model showed that some of the round peas were like the parental round seeded plants and some were like the F1 round seeded plants. Specifically, the model indicated that 1/3 of the F2 round seeded plants should be like parental round seeded plants in terms of factor makeup and 2/3 should be like F1 round seeded plants. Finally, the model indicated that all wrinkled seeded plants from all generations in the cross always carried only factors for wrinkledness. (Examine the model carefully to convince yourself of the truth of these statements.)
There are two very interesting aspects to these claims drawn from the model. First, they are claims regarding the existence and behavior of entities that could not be detected by any methods available at the time, and therefore they deal with theoretical entities and cannot be tested directly. Second, although not subject to direct test, they can be tested indirectly through the derivation of predictions regarding results that can be observed. Specifically, if these claims regarding factor makeup (and the rest of the model) are correct, then it would be possible to predict with precision the types and frequencies of progeny to be expected from certain crosses. Thus, Mendel generated and tested two predictions:
1.If any F1 round seeded plant is crossed with any wrinkled seeded plant, half of the progeny produced will be round, half wrinkled.
2.If many of the F2 round seeded plants are allowed to self fertilize, 1/3 of them should breed true (i.e., produce only round seeded progeny), whereas 2/3 of them should produce both round and wrinkled progeny in a 3:1 ratio.
These predictions were excellent tests of the model because they were clear and precise and because they were unlikely to prove true unless the model was correct. (As an exercise, you should examine the model and then diagram the crosses of both predictions to see why they do follow from the model.)
Mendel carried out the appropriate crosses and in both cases the predictions came true. Because these predictions regarding progeny frequency were derived from Mendel's hypothesis regarding the existence and behavior of unseen factors, the fulfillment of the predictions strengthened Mendel's belief in the validity of his hypothesis. The generation (and testing) of predictions with observable results from hypotheses involving entities that cannot easily be observed directly is common in all genetic research. Therefore, you should make sure that you understand the validity of this reasoning, as its mastery is essential for the mastery of genetics.
ESP Picks from Around the Web (updated 28 JUL 2024 )
Old Science

Weird Science

Treating Disease with Fecal Transplantation
Fossils of miniature humans (hobbits) discovered in Indonesia
Paleontology

Dinosaur tail, complete with feathers, found preserved in amber.
Astronomy

Mysterious fast radio burst (FRB) detected in the distant universe.
Big Data & Informatics

Big Data: Buzzword or Big Deal?
Hacking the genome: Identifying anonymized human subjects using publicly available data.